Problem 170: The height above ground of an object moving vertically is given by
(1) ![]()
with ![]() in feet and
in feet and ![]() in seconds. Find
in seconds. Find
a. the object’s velocity when ![]()
b. its maximum height and when it occurs;
c. its velocity when ![]() .
.
Solution:
a) The object’s velocity is the derivative of the position. That is, when ![]() ,
,
(2) ![]()
b) The maximum height of the object is given when ![]() . That is, solving for
. That is, solving for ![]() ,
,
(3) ![]()
The maximum height happens at the maximum time (t=3). Thus
(4) ![]()
c) When ![]() ,
,
(5) 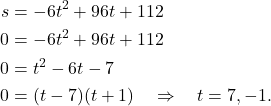
Since ![]() , we take
, we take ![]() . That is, the velocity when
. That is, the velocity when ![]() is given by
is given by
(6) ![]()

Leave a Reply