Derivatives in Applications

Problem 169: A rectangle plot of farmland will be bounded on one side by river and on the other three sides by a single-strand electric fence. With 800 m of wire at your disposal, what is the largest area you can enclose, and what are its dimensions?

Solution: Let $x$ be the length of the rectangle and $y$ be the width. The area of the rectangle is given by

(1) $\begin{equation*} A = x \cdot y. \end{equation*}$

One side of our rectangle is covered by the river. We now need to use the 80 m long wire to cover our other three sides. This means that the perimeter of the rectangle is given by

(2) $\begin{equation*} 800 = 2x + y \quad \Rightarrow \quad y = 800 - 2x. \end{equation*}$

Plugging into (1)

(3) $\begin{align*} A & = x \cdot y \\ & = x \cdot (800-2x) \\ & = 800x - 2x^2.\end{align*}$

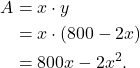
The largest area that can be enclosed is given when the derivative $dA/dx$ is equal to 0. Then

(4) $\begin{equation*} \frac{dA}{dx} = 800 - 4x \quad \Rightarrow \quad x = 200. \end{equation*}$

Now that we know $x=200$ , we can find $y$ .

(5) $\begin{equation*} y = 800 -2x = 800 -2(200) = 400. \end{equation*}$

Hence, the largest area that can be enclosed is $400 \cdot 200 = 800,000 \ m^2$ . The dimensions of the rectangle are 200 of lenght and 400 of width

Leave a Reply Cancel reply