Problem 168: Find the linearization of ![]() at
at ![]() :
:
(1) ![]()
Solution: The linearization of a differentiable function at a point is given by
(2) ![]()
Hence,
(3) 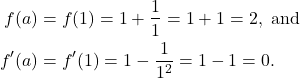
Therefore,
(4) 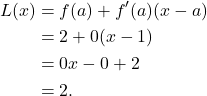
That is,
(5) ![]()

Problem 168: Find the linearization of ![]() at
at ![]() :
:
(1) ![]()
Solution: The linearization of a differentiable function at a point is given by
(2) ![]()
Hence,
(3) 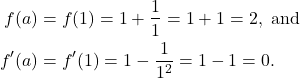
Therefore,
(4) 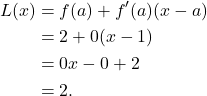
That is,
(5) ![]()
Leave a Reply