Problem 166: Two airplanes are flying in the air at the same height: airplane ![]() is flying east at 250 miles per hour and airplane
is flying east at 250 miles per hour and airplane ![]() is flying north at 300 miles per hour. If they are both heading to the same airport, located 30 miles east of airplane
is flying north at 300 miles per hour. If they are both heading to the same airport, located 30 miles east of airplane ![]() and 40 miles north of airplane
and 40 miles north of airplane ![]() , at what rate is the distance between the airplanes changing?
, at what rate is the distance between the airplanes changing?
Solution: The two airplanes make a right triangle where the length of the two sides are given: ![]() and
and ![]() . Finding the hypotenuse
. Finding the hypotenuse
(1) ![]()
We need to find ![]() . Then
. Then
(2) 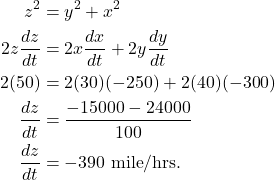
Note that ![]() is negative because the distance between them is decreasing. Hence, the distance between the airplanes is changing at a rate of 390 miles/hrs.
is negative because the distance between them is decreasing. Hence, the distance between the airplanes is changing at a rate of 390 miles/hrs.

Leave a Reply