Problem 165: A 10ft ladder is leaning against a wall. If the top of the ladder slides down the wall at a rate of 2ft per sec, how fast is the bottom of the ladder moving away from the wall when the bottom of the ladder is 5ft from the wall?
Solution: The ladder and the wall make a right triangle. We are given the length of one side ![]() ft and the length of the hypotenuse
ft and the length of the hypotenuse ![]() ft. That is, we find the other side
ft. That is, we find the other side
(1) ![]()
We are asked to find ![]() . Thus
. Thus
(2) 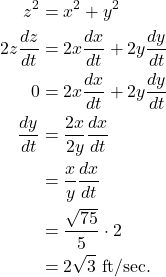
Note that ![]() because the
because the ![]() direction does not change, and
direction does not change, and ![]() is negative since the ladder is sliding down. That is, the bottom of the ladder is moving at a rate of
is negative since the ladder is sliding down. That is, the bottom of the ladder is moving at a rate of ![]() .
.

Leave a Reply