Related Rates Problem II

Problem 164: A hot air ballon rising straight up from a level field is tracked by a range finder 150 m from the liftoff point. At the moment the range finder’s elevation angle is $\pi/4$ , the angle is increasing at the rate of $0.14$ rad/min. How fast is the ballon rising at that moment?

Solution: When solving related rates problem, the first thing we need to do, if possible, is to draw a picture. In this case we have a right-triangle where the angle made by the finder and the ground is $\pi/4$ . Also, the distance of the balloon from the ground is given by $y$ , and the finder is 150 m away from the balloon.

We need to find $dy/dt$ . That is,

(1) $\begin{align*} \tan(\theta) = \frac{y}{150} \quad \Rightarrow \quad y = 150 \tan(\theta) \quad \Rightarrow \quad \frac{dy}{dt} = \frac{d}{dt} (150 \tan \theta).\end{align*}$

We know that $\theta = \pi/4$ and $d\theta/dt = 0.14$ rad/min so that

(2) $\begin{align*}\frac{d\thetha}{dt} & = \sec^2(\theta) \cdot \frac{d\theta}{dt} \\ & = 150 \cdot \left(\sec(\pi/4)\right)^2 \cdot (0.14) \\ & = 150(\sqrt{2})^2(0.14) \\ & = 42 \ \text{m}/\text{min}.\end{align*}$

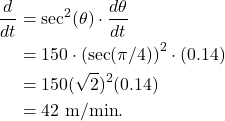
Thus the balloon is increasing at a rate of 42 m/min.

Leave a Reply Cancel reply