Problem 161: Show that ![]() where
where ![]() and
and ![]() is a differentiable function of
is a differentiable function of ![]() .
.
Solution: Using the relationship between ![]() and
and ![]() ,
,
(1) ![]()
Then
(2) 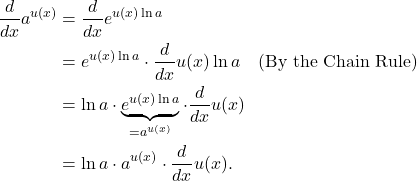
That is,
(3) ![]()

Problem 161: Show that ![]() where
where ![]() and
and ![]() is a differentiable function of
is a differentiable function of ![]() .
.
Solution: Using the relationship between ![]() and
and ![]() ,
,
(1) ![]()
Then
(2) 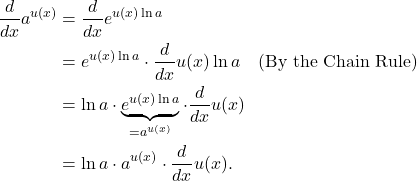
That is,
(3) ![]()
Leave a Reply