Problem 159: Using mathematical induction, show that for ![]()
(1) ![]()
Solution: Since we will use mathematical induction to prove (1), we need to prove the base case and the inductive case. That is,
Base Case: Let ![]() . Then
. Then
(2) 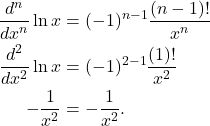
Inductive Case: We assume that (1) holds for ![]() . We will show that it also holds for
. We will show that it also holds for ![]() . That is,
. That is,
(3) 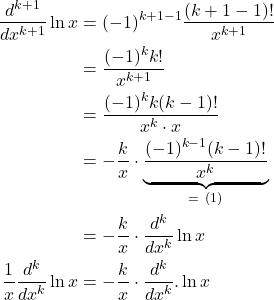
It must be the case that ![]() so that it proves (1).
so that it proves (1).

Leave a Reply