Problem 158: Use the Identity
(1) ![]()
to derive the formula for the derivative of ![]() .
.
Solution: Using the identity (1), we have
(2) 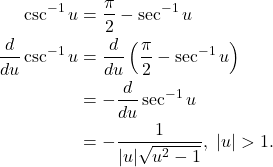
That is,
(3) ![]()

Problem 158: Use the Identity
(1) ![]()
to derive the formula for the derivative of ![]() .
.
Solution: Using the identity (1), we have
(2) 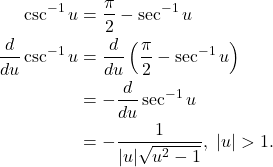
That is,
(3) ![]()
Leave a Reply