Differentiability at a Point

Problem 155: Show that the function $y = |x|$ is differentiable on $(-\infty, 0)$ and on $(0, \infty)$ but has no derivative at $x = 0$ .

Solution: A function is differentiable if the function has a derivative. That is,

(1) On $(-\infty, 0)$ , $y = |x| = -x$ . Then $y' = -1$ . Therefore, on $(-\infty, 0)$ , the function has derivative -1.

(2) On $(0, \infty)$ , $y = |x| = x$ . Then $y' = 1$ . Therefore, on $(0,\infty)$ , the function has derivative 1.

(3) In order for the function to have a derivative at $x = 0$ , the two sided limits need to agree.

That is, from the right sided,

(1) $\begin{align*} f'(x) & = \lim_{h \to 0^{+}} \frac{f(x+h)-f(x)}{h} \\ & = \lim_{h \to 0^{+}} \frac{|x+h|-|x|}{h} \\ & = \lim_{h \to 0^{+}} \frac{|0+h|-|0|}{h} \ \text{at} \ x = 0 \\ & = \lim_{h \to 0^{+}} \frac{|h|}{h} \\ & = \lim_{h \to 0^{+}} \frac{h}{h}, \quad |h| = h \ \text{when} \ h \to 0^{+} \\ & = 1. \end{align*}$

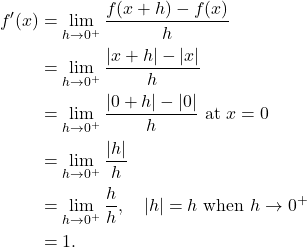
From the left hand sided,

(2) $\begin{align*} f'(x) & = \lim_{h \to 0^{-}} \frac{f(x+h)-f(x)}{h} \\ & = \lim_{h \to 0^{-}} \frac{|x+h|-|x|}{h} \\ & = \lim_{h \to 0^{-}} \frac{|0+h|-|0|}{h} \ \text{at} \ x = 0 \\ & = \lim_{h \to 0^{-}} \frac{|h|}{h} \\ & = \lim_{h \to 0^{-}} -\frac{h}{h}, \quad |h| = -h \ \text{when} \ h \to 0^{-} \\ & = -1. \end{align*}$

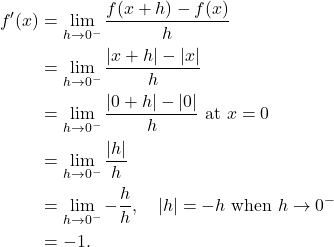
Since $\lim_{h \to 0^{+}} f(x) \ne \lim_{h \to 0^{-}} f(x)$ , $\lim_{h \to 0} f(x)$ do not exist. Hence, $f(x)$ is not differentiable at $x=0$ .

Leave a Reply Cancel reply