Derivative as a Rate of Change II

Problem 154: It takes 12 hours to drain a storage tank by opening the valve at the bottom. The depth $y$ of fluid in the tank $t$ hours after the valve is opened is given by the formula

(1) $\begin{equation*} y = 6 \left( 1- \frac{t}{12} \right)^2 \ \text{m}. \end{equation*}$

a. Find the rate $dy/dt$ (m/h) at which the tank is draining at time $t$ .

b. When is the fluid level in the tank falling fastest? Slowest? What are the values of $dy/dt$ at these times?

Solution:

a. By the chain rule,

(2) $\begin{align*} y & = 6 \left( 1- \frac{t}{12} \right)^2 \\ \frac{dy}{dx} & = 2\cdot 6 \cdot \left( 1-\frac{t}{12}\right) \cdot \left(-\frac{1}{12} \right) \\ & = \frac{t}{12} -1 .\end{align*}$

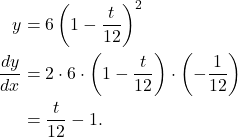
That is, the tank is draining at a rate of

(3) $\begin{equation*} \frac{dy}{dt} = \frac{t}{12} - 1 \quad \text{m/h}. \end{equation*}$

b. When $t = 0$ , $\frac{dy}{dx} = -1$ (m/h), and when $t = 12$ , $\frac{dy}{dx} = 0$ (m/h). Therefore, the smallest value is at t = 0 h and the largest at t = 12 h.

Leave a Reply Cancel reply