Perimeter of an Isosceles Triangle

Problem 152: The perimeter of an enclosed isosceles triangle is 40 feet. The length of the shortest side is 7 less than half of the two longest (equal) sides. What are the length of the sides of the enclosure?

Solution: The perimeter of an isosceles triangle is given by

(1) $\begin{equation*} P = 2x + y, \end{equation*}$

where $P$ is the perimeter, $x$ is the length of the two equal sides, and $y$ is the base (the length of the shortest side).

We are given that the perimeter is 40 feet ( $P = 40$ ), and that the shortest side is 7 less than half of the two longest (equal) sides ( $y = 1/2x -7$ ).

Therefore,

(2) $\begin{align*} P & = 2x+ y \\ 40 & = 2x + \frac{1}{2}x - 7 \\ 40 & = \frac{5}{2}x - 7 \\ \frac{5}{2}x & = 47 \\ x & = \frac{94}{5}. \end{align*}$

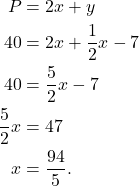
Hence, the sides length is 94/5 ft.

Leave a Reply Cancel reply