Perimeter of a Rectangle

Problem 151: A rectangle garden has a length that is 10 feet longer than its width. The perimeter is 42 feet. Wat are the dimensions of the garden?

Solution: The perimeter of a rectangle is given by

(1) $\begin{equation*} P = 2x + 2y, \end{equation*}$

where $P$ is the perimeter, $x$ is the length of the sides, and $y$ is the width.

We are given that the length of the rectangle garden is 10 feet longer than its width. That is, this means that $x = y + 10$ . Therefore,

(2) $\begin{align*} P & = 2x + 2y \\ & = 2(y + 10) + 2y \\ & = 4y + 10. \end{align*}$

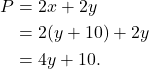
Since the perimeter is 42 feet,

(3) $\begin{align*} P & = 4y + 10 \\ 42 & = 4y + 10 \\ 4y & = 42-10 \\ y& = \frac{22}{4} \\ & = 5.5.\end{align*}$

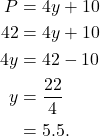
Using (1),

(4) $\begin{align*} P & = 2x + 2y \\ 42 & = 2x + 2(5.5) \\2x & = 42 - 2(5.5) \\ x & = 15.5.\end{align*}$

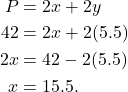
Hence, the length of the garden is 15.5 ft and the width is 5.5 ft.

Leave a Reply Cancel reply