The Sandwich Theorem

Problem 141: If $\sqrt{5-2x^2} \le f(x) \le \sqrt{5-x^2}$ for $-1 \le x \le 1$ , find $\lim_{x \to 0} f(x)$ .

Solution: Since $f(x)$ is bounded by two functions, says $g(x) = \sqrt{5-2x^2}$ and $h(x) = \sqrt{5-x^2}$ , we will use the Sandwich Theorem to find our limit.

The Sandwich Theorem: Suppose that $g(x) \le f(x) \le h(x)$ for all $x$ in some open interval containing $c$ , except possibly at $x = c$ itself. Suppose also that $\lim_{x \to c} g(x) = \lim_{x \to c} h(x) = L$ . Then $\lim_{x \to c} f(x) = L$ .

That is, since we are interested in the limit approaching $0$ which is in the interested interval,

(1) $\begin{align*}\lim_{x \to 0} g(x) & = \lim_{x \to 0} \sqrt{5-2x^2} =\sqrt{5-0} = \sqrt{5} \\ \lim_{x \to 0} h(x) & = \lim_{x \to 0} \sqrt{5-x^2} =\sqrt{5-0} = \sqrt{5}. \end{align*}$

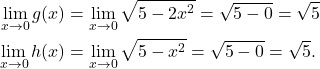
By The Sandwish Theorem,

(2) $\begin{equation*} \lim_{x \to 0} f(x) = \sqrt{5}. \end{equation*}$

Leave a Reply Cancel reply