Average Speed

Problem 139: A rock breaks loose from the top of a tall cliff. What is its average speed

(a) during its first 2 sec of fall?

(b) during the 1-sec interval between second 1 and second 2?

Solution: The average speed (S) of a function $f(x)$ over the interval $[t_1, t_2]$ is given by

(1) $\begin{equation*} S = \frac{f(t_2)-f(t_1)}{t_2-t_1}.\end{equation*}$

(a) Using Galileo Law, the distance travel by an object from free fall is given by $y = 16t^2$ ft. That is, in this case $t_1=0$ and $t_2=2$ . Thus

(2) $\begin{align*} S & = \frac{f(t_2)-f(t_1)}{t_2-t_1} \\ & = \frac{16(2)^2 - 16(0)^2}{2-0} \ \text{ft/s} \\ & = 32 \ \text{ft/s}. \end{align*}$

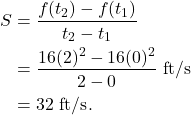
(b) In this case, $t_1=1$ and $t_2=2$ so that

(3) $\begin{align*} S & = \frac{f(t_2)-f(t_1)}{t_2-t_1} \\ & = \frac{16(2)^2 - 16(1)^2}{2-1} \ \text{ft/s} \\ & = 48 \ \text{ft/s}. \end{align*}$

Leave a Reply Cancel reply