Problem 138: Evaluate the following complex integral
(1) ![]()
Solution: When evaluating complex integral, we consider the real part and imaginary part of the integral separately. That is,
(2) 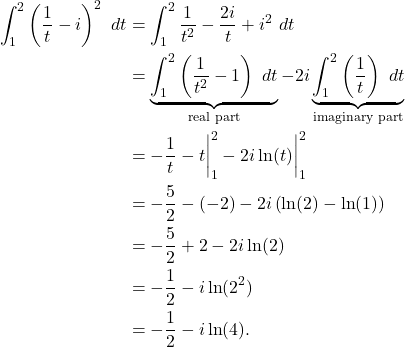
That is,
(3) ![]()

Problem 138: Evaluate the following complex integral
(1) ![]()
Solution: When evaluating complex integral, we consider the real part and imaginary part of the integral separately. That is,
(2) 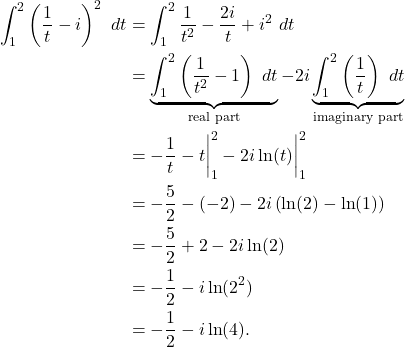
That is,
(3) ![]()
Leave a Reply