Basis of Null Space

Problem 134: Find the basis for the null space of

(1) $\begin{equation*} A = \begin{bmatrix} 1 & 2 & 0 \\ 0 & 5 & 1 \\ 3& 1 & -1 \end{bmatrix}. \end{equation*}$

Solution: In order to find the null space of the given matrix, we first need to make the matrix in row reduced echelon form. That is, when we row reduced the matrix $A$ , we get the following matrix

(2) $\begin{align*} \begin{bmatrix} 1 & 0 & -2/5 \\ 0 & 1 & 1/5 \\ 0& 0 & 0 \end{bmatrix}.\end{align*}$

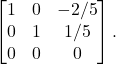
Since we are looking for the null space, we have

(3) $\begin{align*} \begin{bmatrix} 1 & 0 & -2/5 \\ 0 & 1 & 1/5 \\ 0& 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} x_1 \\ x_2 \\ x_3\end{bmatrix} & = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}.\end{align*}$

Multiplying the matrices we get

(4) $\begin{align*} x_1 + 0x_2 - 2/5x_3 & = 0 \quad \Rightarrow \quad x_1 =2/5x_3 \\ 0x_1 + x_2 + 1/5x_3 & = 0 \quad \Rightarrow \quad x_2=-1/5x_3. \end{align*}$

Note that we are solving the pivot columns in term of the free variable. Thus

(5) $\begin{align*} \begin{bmatrix} x_1 \\ x_2 \\x_3\end{bmatrix} & = \begin{bmatrix} 2/5x_1 \\ -1/5x_2 \\x_3 \end{bmatrix} \\ & = x_3\begin{bmatrix} 2/5 \\ -1/5\\ 1\end{bmatrix}. \end{align*}$

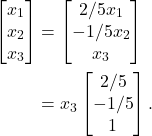
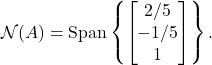
What does this mean? This means that basis for the null space if given by

(6) $\begin{equation*} \mathcal{N}(A) = \text{Span} \left\{ \begin{bmatrix}2/5 \\ -1/5 \\1 \end{bmatrix} \right\}.\end{equation*}$

Leave a Reply Cancel reply