Problem 132: Determine if ![]() is a subspace of
is a subspace of ![]() .
.
Solution: If ![]() is a subspace, then it must meets the following three conditions.
is a subspace, then it must meets the following three conditions.
- The zero vector must be in
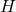 . That is, let
. That is, let 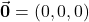 . Thus
. Thus (1)
Since the zero vector satisfies the equation, this means that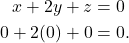
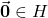 .
. 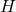 must be closed under addition. That is,
must be closed under addition. That is, 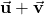 must be in
must be in 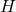 for any two vectors
for any two vectors 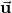 and
and 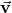 . Let
. Let 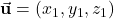 and
and 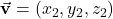 . Then
. Then (2)
Hence,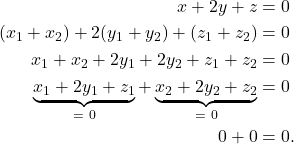
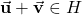 .
.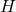 must be closed under scalar multiplication. That is,
must be closed under scalar multiplication. That is, 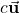 must be in
must be in 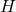 for any scalar
for any scalar 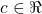 and vector
and vector 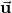 . That is, let
. That is, let 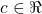 and
and 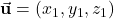 so that
so that 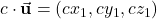 . That is,
. That is, (3)
Therefore,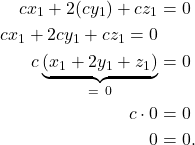
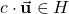 .
.
Indeed, ![]() is a subspace of
is a subspace of ![]() .
.

Leave a Reply