Problem 129: Consider the initial value problem
(1) ![]()
(a) Take the Laplace transform of both sides of the given differential equation to create the corresponding algebraic equation. Denote the Laplace transform of ![]() by
by ![]() .
.
(b) Solve your equation for ![]() .
.
Solution: First, let’s highlights some of the things we need to solve this problem. That is,
(2) 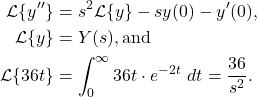
(a) Let’s now find the corresponding Laplace transform.
(3) 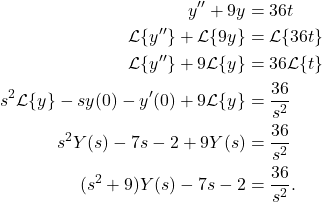
(b) One can now some for ![]() .
.
(4) 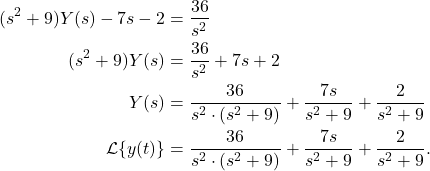
That is, we can now find the solution ![]() by taking the inverse Laplace transform.
by taking the inverse Laplace transform.
(5) ![]()

Leave a Reply