Problem 128:
(a) Find the general solution to ![]()
(b) Find the particular solution that satisfies ![]() and
and ![]() .
.
Solution: The general solution of a second order ODE with repeated roots is given by
(1) ![]()
where ![]() and
and ![]() are the roots of the characteristic polynomial.
are the roots of the characteristic polynomial.
(a) Let ![]() so that
so that ![]() and
and ![]() . This means that
. This means that
(2) 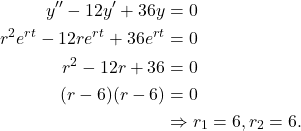
Hence, using (1), the general solution is given by
(3) ![]()
(b) Let’s now find the particular solution. First, we will find ![]() using the condition
using the condition ![]() .
.
(4) 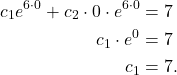
Then (3) takes the following form
(5) ![]()
Using our second condition, that is, ![]()
(6) 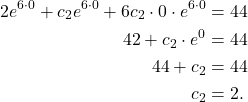
Therefore, the particular solution is given by
(7) ![]()

Leave a Reply