Second Order ODE with Basic Roots

Problem 124: Given the second order ODE

(1) $\begin{equation*} y'' + 8y' + 7 y = 0, \end{equation*}$

find the solutions $y_1(x)$ and $y_2(x)$ .

Solution: The general solution of a second order ODE with basic root is given by

(2) $\begin{equation*} y = y_1(x) + y_2(x) = c_1 \cdot e^{r_1 x} + c_2 \cdot e^{r_2 x},\end{equation*}$

where $c_1$ and $c_2$ are arbitrary constant, $r_1$ and $r_2$ are the complex roots of the characteristic polynomial. Finding the roots of the characteristic polynomial gives us

(3) $\begin{align*} y'' + 8y' + 7 y & = 0 \\ r^2 + 8r + 7 & = 0 \\ & \Rightarrow r = -7, -1. \quad \text{(the roots)}\end{align*}$

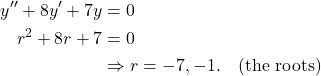
That is,

(4) $\begin{align*}y_1(x) & = c_1 \cdot e^{r_1 x} \\ & = c_1 \cdot e^{-7x}. \left \end{align*}$

Similarly,

(5) $\begin{align*}y_2(x) & = c_2 \cdot e^{r_2 x} \\ & = c_2 \cdot e^{-x}. \end{align*}$

NOTE: Since this is a linear ODE, one can add the two solutions in order to get a general solution, but I will just give the two solutions separately.

Hence,

(6) $\begin{align*} y_1(x) & = c_1 e^{-7x}, \quad \text{and} \\ y_2(x) & = c_2e^{-x}. \end{align*}$

Leave a Reply Cancel reply