Problem 123: Given the second order ODE
(1) ![]()
find the solutions ![]() and
and ![]() .
.
Solution: The general solution of a second order ODE with complex root is given by
(2) ![]()
where ![]() and
and ![]() are arbitrary constant,
are arbitrary constant, ![]() and
and ![]() are the complex roots of the characteristic polynomial. Finding the roots of the characteristic polynomial gives us
are the complex roots of the characteristic polynomial. Finding the roots of the characteristic polynomial gives us
(3) 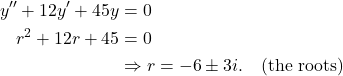
That is,
(4) 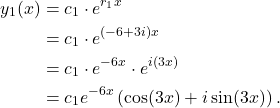
Similarly,
(5) 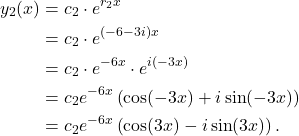
NOTE: Since this is a linear ODE, one can add the two solutions in order to get a general solution, but I will just give the two solutions separately. Also, a little bit of more simplification can be obtained, but for simplicity it will not be done.
Hence,
(6) 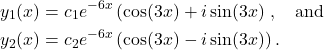

Leave a Reply