Problem 119: Verify the identity:
(1) ![]()
Solution: If we want to verify this equation, we need to pick a side in order to prove the other side. I will start with the left-hand side ![]() and show that it is equal to the right-hand side
and show that it is equal to the right-hand side ![]() . That is,
. That is,
(2) 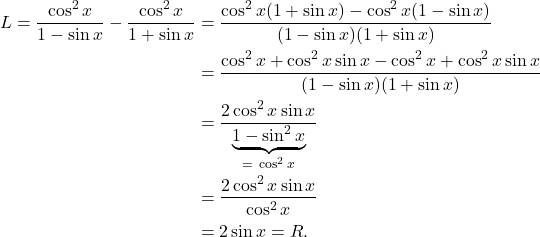
Hence, ![]() as desired.
as desired.

Leave a Reply