Linearization

Problem 118: Find the linearization $L(x)$ of the function at $a$ .

(1) $\begin{equation*} f(x) = \sqrt[3]{x}, \quad a = -8 \end{equation*}$

Solution: The linearization is given by $L(x) = f(a) + f'(a)(x-a)$ . Thus we will find the pieces of the formula and then assemble them. That is,

(2) $\begin{equation*} f(a) = f(-8) = \sqrt[3]{-8} = \sqrt[3]{(-2)^3} = -2. \end{equation*}$

We must now find the derivative evaluated at $a = -8$ .

(3) $\begin{align*} f(x) & = x^{1/3} \\ f'(x) & = \frac{1}{3} \cdot x^{-2/3} \\ & = \frac{1}{3} \cdot \frac{1}{x^{2/3}} \\ & = \frac{1}{3} \cdot \frac{1}{\sqrt[3]{x^2}} \end{align*}$

Hence,

(4) $\begin{align*} f'(x) & = \frac{1}{3} \cdot \frac{1}{\sqrt[3]{x^2}} \\ f'(a) & = \frac{1}{3} \cdot \frac{1}{\sqrt[3]{(-8)^2}} \\ & = \frac{1}{3} \cdot \frac{1}{\sqrt[3]{64}} \\ & = \frac{1}{3} \cdot \frac{1}{4} \\ & = \frac{1}{12}. \end{align*}$

One can now find the linearization.

(5) $\begin{align*} L(x) & = f(a) + f'(a)(x-a) \\ & = -2 + \frac{1}{12} \cdot (x-(-8)) \\ & = -2 + \frac{1}{12}x + \frac{8}{12} \\ & = \frac{1}{12}x - \frac{4}{3}. \end{align*}$

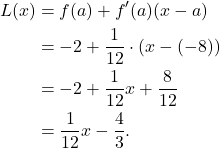
Therefore,

(6) $\begin{equation*} \boxed{L(x) = \frac{1}{12}x - \frac{4}{3}}. \end{equation*}$

Leave a Reply Cancel reply