Problem 116: Find ![]() using the method of logarithmic differentiation when
using the method of logarithmic differentiation when ![]() .
.
Solution: We need to use property of logarithm to solve this problem. That is,
(1) 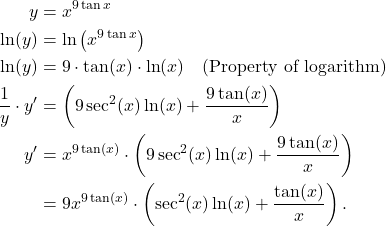
Hence,
(2) 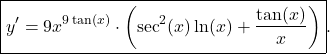

Problem 116: Find ![]() using the method of logarithmic differentiation when
using the method of logarithmic differentiation when ![]() .
.
Solution: We need to use property of logarithm to solve this problem. That is,
(1) 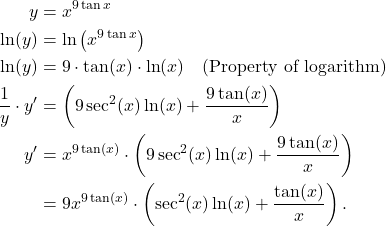
Hence,
(2) 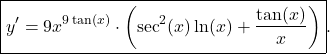
Leave a Reply