Bayes’ Theorem

Problem 115: The New York Times of January 24, 1997, discussed the recommendation of a special panel concerning mammograms for women in their 40s. About 2% of women aged 40 to 49 years old develop breast cancer in their 40s. But the mammogram used for women in that age group has a high rate o false positives and false negatives; the false positive rate is .30, and the false negative rate is .25. If a woman in her 40s has a positive mammogram, what is the probability that she actually has breast cancer?

Solution: First, let’s define some events. Let A = “she (the woman) actually has breast cancer” and B = “she (women) in her 40s has a positive mammogram”. Having our events defined, we will use Bayes’ Theorem of calculate the probability. That is, we want to calculate

(1) $\begin{equation*} P(A|B) = \frac{P(A) \cdot P(B|A)}{P(A) \cdot P(B|A) + P(A^c) \cdot P(B|A^c)}. \end{equation*}$

Now that we know that we will be using Baye’s Theorem, we need to find our corresponding values from the problem.

(2) $\begin{align*} P(A) & = 2 \% = 0.02 \\ P(B|A) & = 1- \text{(false negative rates)}= 1-P(B^c|A) = 1- .25 = .75 \\ P(A^c) & = 1 - P(A) = 1 -0.02 = 0.98 \\ P(B|A^c) & = \text{false positive rate} = .30. \end{align*}$

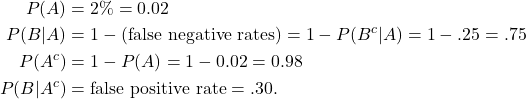
Therefore,

(3) $\begin{align*} P(A|B) & = \frac{P(A) \cdot P(B|A)}{P(A) \cdot P(B|A) + P(A^c) \cdot P(B|A^c)} \\ & = \frac{(0.02)(0.75)}{(0.02)(0.75) + (0.30)(0.98)} \\ & = \frac{0.015}{0.015 + 0.294} \\ & = \frac{0.015}{0.309} \\ & \approx 0.049.\end{align*}$

Hence, the probability that she actually has breast cancer is about 4.9%.

Leave a Reply Cancel reply