Dependent Event

Problem 113: A sample of two balls is drawn from an urn containing two white balls and three red balls. Are the events

A = “the sample contains at least one white ball” and B = “the sample contains balls of both colors” independent?

Solution: If events $A$ and $B$ are independent, then $P(A|B) = P(A)$ and $P(B|A) = P(B)$ .

1. Calculate $P(A)$ :

(1) $\begin{align*} P(A ) & = \frac{\text{at least one white ball}}{\text{number of selected ball}} \\ & = \frac{\binom{2}{1} \cdot \binom{3}{1} + \binom{2}{2} \cdot \binom{3}{0}}{\binom{5}{2}} \\ & = \frac{7}{10}. \end{align*}$

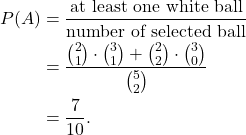
2. Calculate $P(B)$ :

(2) $\begin{align*} P(B) & = \frac{\text{balls of both colors}}{\text{number of selected ball}} \\ & = \frac{\binom{2}{1} \cdot \binom{3}{1}}{\binom{5}{2}} \\ & = \frac{6}{10}. \end{align*}$

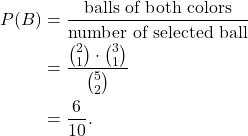
3. Calculate $P(A|B)$ :

(3) $\begin{align*} P(A|B) & = \frac{P(A \cap B)}{P(B)} \\ & = \frac{\text{at least one white ball and balls of both colors}}{\text{number of selected ball}} \\ & = \frac{P(B)}{P(B)} \\ & = 1. \end{align*}$

4. Calculate $P(B|A)$ :

(4) $\begin{align*} P(B|A) & = \frac{P(B \cap A)}{P(A)} \\ & = \frac{\text{balls of both colors and at least one white ball}}{\text{number of selected ball}} \\ & = \frac{6/10}{7/10} \\ & = \frac{6}{7}. \end{align*}$

Since $P(A|B) \ne P(A)$ and $P(B|A) \ne P(B)$ , the events $A$ and $B$ are not independent.

Leave a Reply Cancel reply