Volume of an Sphere and Cone

Problem 106: Find the volume of a half sphere (radius 5 yds) on the base of an inverted cone with the same radius and height of 7 yds.

Solution: We will solve this problem by finding the volume of the shapes separately and then add them.

The volume of an sphere is given by $V_{\text{whole sphere}} = 4/3 \pi r^3$ . Since we are given only half of the sphere,

(1) $\begin{equation*} V_{\text{half sphere}} = \frac{1}{2} \cdot V_{\text{whole sphere}} = \frac{1}{2} \cdot \frac{4}{3} \cdot \pi \cdot r^3 = \frac{2}{3} \pi r^3. \end{equation*}$

The volume of a cone is given by

(2) $\begin{equation*} V_{\text{cone}} = \frac{1}{3} \pi r^2 h.\end{equation*}$

Hence, the volume of the asked shape is given by

(3) $\begin{align*} V & = V_{\text{half sphere}} + V_{\text{cone}} \\ & = \frac{2}{3} \pi (5 \ \text{yds})^3 + \frac{1}{3} \pi (5 \ \text{yds})^2 (7 \ \text{yds}) \\ & = \frac{250 \pi}{3} \ \text{(yds)}^3 + \frac{175 \pi}{3} \ \text{(yds)}^3 \\ & = \frac{425 \pi}{3} \ \text{(yds)}^3 \\ & \approx 445.06 \ \text{(yds)}^3. \end{align*}$

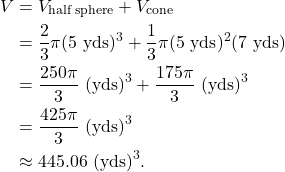
That is,

(4) $\begin{equation*} V \approx 445.06 \ \text{(yds)}^3. \end{equation*}$

Leave a Reply Cancel reply