Th Binomial Theorem

Problem 104: Expand $(x+y)^6$ .

Solution: If we want to expand this, we can either multiply it out 6 times or use the binomial theorem. We will use the latter here. That is,

$\begin{align*} (x+y)^6 & = \binom{6}{0}x^6 + \binom{6}{1} x^5y + \binom{6}{2} x^4y^2 + \binom{6}{3}x^3y^3 + \binom{6}{4}x^2y^4 + \binom{6}{5}xy^5 \\ & = 1 \cdot x^6 + 6 \cdot x^5y + 15 \cdot x^4 y^2 + 20 \cdot x^3y^3 + 15 \cdot x^2y^4 + 6 \cdot xy^5 + 1 \cdot y^6.\end{align*}$

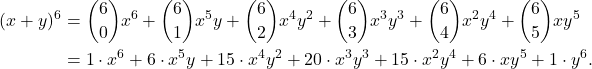
Note that by using the binomial theorem, we just had to calculate the coefficients.

Leave a Reply Cancel reply